Phonons are quasi-particles that quantize the energy of lattice vibrations. The concept of phonon has been developed by Albert Einstein, Peter Joseph William Debye, Max Born, Theodore von Kármán, etc., and was formally named by Jacov Frenkel in 1932. In history, the Debye model has played a pivotal role, but it is only applicable to linearly dispersive phonons.

Recently, the research team led by Prof. Minqiang JIANG from the Institute of Mechanics, Chinese Academy of Sciences, proposes a unified theory of phonon in solids to show when the Debye model breaks down as Van Hove singularities in crystals, the boson peaks in glasses, or their coexistence. This study entitled “Unified Theory of Phonons in Solids with Phase Diagram of non-Debye Anomalies” has been published in Nature Physics.

To explain why the Dulong-Petit law fails to describe the heat capacity of solids at very low temperatures, Einstein in 1907 applied Planck's quantum hypothesis to quantize the energy of lattice vibrations (i.e., the concept of "phonons" later). However, due to the neglect of phonons’ interaction, the Einstein model only qualitatively matched experimental observations. In 1912, Debye improved the Einstein theory by treating low-frequency phonons as continuum elastic waves, and derived the vibrational density of states (VDOS) as proportional to the squared frequency. The Debye model successfully predicts phononic contribution to the specific heat of solids in the continuum limit.

However, as the phonon wavenumber increases, the VDOS gradually deviates from the Debye prediction and eventually manifests as the Van Hove singularities (VHS) for crystals, and a boson peak (BP) for glasses. These non-Debye anomalies have a profound influence on the low-temperature properties of solids, such as specific heat, thermal conductivity, superconductivity and plasticity. In the past decades, there is much controversy over whether these two non-Debye anomalies: VHS and BP are equivalent or not.

In this study, the research team developed a VDOS model universal for solids, either amorphous materials or ordered crystals. The model derives a phonon damping function that not only describes the low-wavenumber Rayleigh scattering but also captures the Mie damping at higher wavenumbers. This damping directly contributes to an extra softening of phonons in dispersion beyond the inherent softening near the (pseudo-) Brillouin zone boundary, which extends the Debye’s linear dispersion to nonlinear regimes.

In the competition between phonon propagation and damping, the model predicts a panoramic “phase diagram” of non-Debye phonon anomalies: BP and VHS. It demonstrates that the continuous softening of phonons induces either single BP or single VHS. The VHS mainly arises from phonon softening near the Brillouin zone boundary, leading to a piling-up of the VDOS. The BP comes from a combined contribution from both extra and inherent softening. Accompanied by the occurrence of BP or VHS, the damping deviates from Rayleigh scattering, and the acoustic behavior is lost. In this sense, the BP can be regarded as a broadened version of the VHS that moves to low frequencies due to extra softening. When the phonon damping/scattering exhibits a resonance peak, the extra softening in dispersion becomes significantly localized and thus separates from inherently global softening. In this scenario, the coexistence of BP and VHS emerges, demonstrating they are fundamentally distinct phenomena.

This unified theory, beyond the Debye model, is further supported by a comparison with experimental heat capacity data over a wide range of real solids, including 143 crystalline and glassy substances. These findings settle a long-standing debate as to the physical relationship between VHS and BP, and deepen our fundamental understanding of the continuum elasticity of real solids.

Phase diagram of non-Debye phonon anomalies: Van Hove singularities and boson peak, based on the unified theory of phonons.

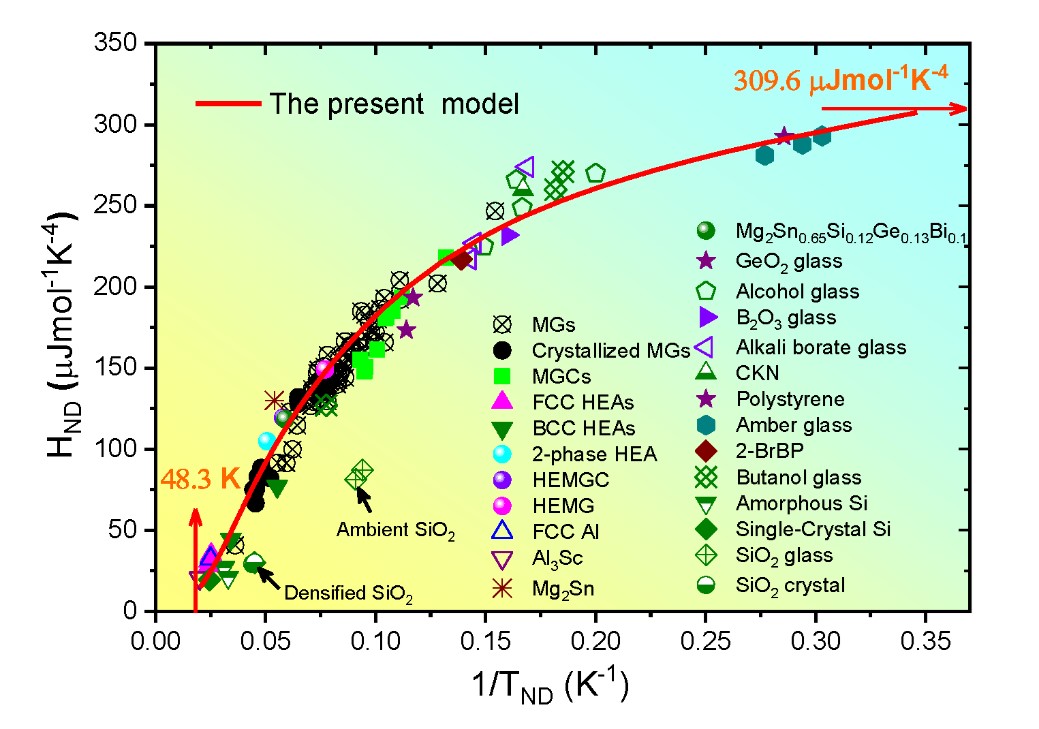
The unified theory is supported by a comparison with experimental heat capacity data over a wide variety of crystalline and glassy solids.

Original link: https://www.nature.com/articles/s41567-025-03057-7

Contact：

ZHANG Ziao

Institute of Mechanics Chinese Academy of Sciences

Tel：86-010-82543676

E-mail：ziaozhang@imech.ac.cn

Web：http://www.imech.cas.cn/